2.1 Lineare Funktionen

Die lineare Funktion ist die einfachste rationale Funktion. Ihre allgemeine Form lautet:

f(x) = mx + t

m wird meist als Steigung und t als Y-Achsenabschnitt der Funktion bezeichnet.

Funktionsverlauf

Lineare Funktionen stellen einfache Geraden dar. Einige Beispiele für lineare Funktionen:

Je größer m gewählt wird, desto steiler richtet sich die Gerade auf. Analog dazu wird die Gerade für kleinere m flacher. Man sollte jedoch beachten, dass man mit der linearen Funktion keine Parallelen zur Y-Achse darstellen kann, da hierzu die Steigung unendlich groß sein müsste. Ist m negativ, ist auch die Steigung der Geraden negativ.

Da t unabhängig von x den Funktionswert erhöht oder erniedrigt, kann man durch t den gesamten Graphen an der Y-Achse entlang verschieben. Dabei kann t natürlich auch kleiner 0 werden. Ist t = 0, geht die Gerade durch den Ursprung.

Berechnung der Steigung und des Y-Achsenabschnittes

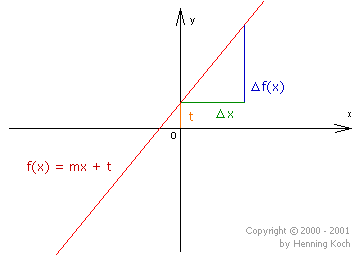Hat man die Gerade gegeben, kann man m erhalten, in dem man mißt, um wie viel sich der Funktionswert für eine Strecke x verändert, und dann die beiden Werte in ein Verhältnis setzt:

m =      y     x      =      f(x)     x

Der Y-Achsenabschnitt t ist der Wert der Funktion bei x = 0:

t = f(0)

Zeichnen des Funktionsgraphen

Zum schnellen Zeichnen des Funktionsgraphen sollte man sich folgende Vorgehensweise einprägen:

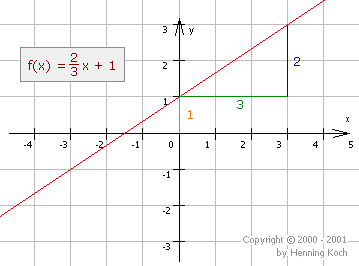
1. Von dem Ursprung aus um t an der Y-Achse entlang gehen. Wir nennen diesen Punkt P₁.
2. Von P₁ aus um den Zähler von m nach oben, und um den Nenner von m nach rechts gehen. Wir nennen diesen Punkt P₂.
3. Der Graph ist eine Gerade durch P₁ und P₂.

Wir wollen dies an einer Beispielfunktion demonstrieren:

Berechnung des Winkels zwischen Gerade und X-Achse

Gesucht ist der Winkel zwischen dem Funktionsgraphen und der X-Achse:

Da x und f(x) ein rechtwinkeliges Dreieck bilden, gelten folgende Beziehungen:

tan() =      f(x)     x      = m     = tan–1(m) = arctan(m)

Schnitt zweier Geraden

Wie alle Funktionen schneidet man zwei Geraden, indem man die beiden Funktionsterme gleichsetzt und nach x auflöst. Den Y-Wert des Schnittpunktes bekommt man dann, indem man die Lösung in eine der beiden Funktionsterme einsetzt.

Zwei aufeinander senkrecht stehende Geraden

Stehen zwei Geraden senkrecht aufeinander, so ergibt das Produkt der beiden Steigungen -1:

m1·m2 = –1 g1 g2

Nullstellen

Eine lineare Funktion hat immer genau eine Nullstelle, ausgenommen für den Sonderfall m = 0, womit f(x) eine konstante Funktion, also eine Parallele zur X-Achse ist.

Zur Berechnung der Nullstellen setzt man f(x) = 0:

mx0 + t = 0     x0 = –      t     m

Einige Aufgaben zu diesem Kapitel warten auf ihre Lösung!

Nächstes Kapitel:
2.2 Quadratische Funktionen