2.3.3 Ableitung ganzrationaler Funktionen

In den folgenden Kapiteln werden wir immer wieder eine Funktion ableiten oder differenzieren müssen - zwei Wörter, die dasselbe meinen. Die Ableitung f'(x) einer Funktion f(x) ist selbst eine Funktion, aus der wir die Steigung von f(x) an einer Stelle ablesen können. Geometrisch kann man die Bedeutung der Ableitung so zusammenfassen:

f'(x0) < 0 f'(x0) = 0 f'(x0) > 0 Graph fällt bei x0 Graph verläuft bei x0 waagrecht Graph steigt bei x0

Die erste Ableitung sagt auch etwas darüber aus, wie steil die Funktion steigt oder fällt:

• Je positiver f'(x₀), desto steiler steigt die Funktion f(x) an der Stelle x₀.
• Je negativer f'(x₀), desto steiler fällt die Funktion f(x) an der Stelle x₀.

An einer Illustration soll die geometrische Beziehung von f(x) und f'(x) verdeutlicht werden. Man denke daran, dass f'(x) nichts direkt mit den Funktionswerten von f(x) zu tun hat, sondern lediglich angibt, ob und wie stark die Funktion steigt oder fällt:

Bildung der Ableitungsfunktion

Die Berechnung von f'(x) ist bei ganzrationalen Funktionen (Polynomen) mit ein paar Rechenregeln recht einfach:

1. Die Ableitung einer Konstanten ist Null

   f(x) = 5 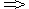  f'(x) = 0 f(x) = -10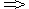 f'(x) = 0 f(x) = 4.5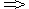 f'(x) = 0

2. Die Ableitung von xⁿ ist n·x^n-1

   f(x) = x5 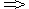f'(x) = 5x5-1 = 5x4 f(x) = x3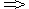 f'(x) = 3x2 f(x) = x1000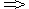 f'(x) = 1000x999 f(x) = x2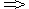 f'(x) = 2x1 = 2x f(x) = x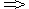 f'(x) = x0 = 1

3. Die Ableitung von C·u(x) ist C·u'(x)

   Ein konstanter Faktor C vor der Funktion bleibt bei der Ableitung erhalten:

   f(x) = 3x6 f'(x) = 3·6x6-1 = 18x5 f(x) = 7x2 f'(x) = 14x f(x) = -2x50 f'(x) = -100x49 f(x) = 8x f'(x) = 1·8·x0 = 8 f(x) = -3x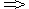 f'(x) = -3

4. Die Ableitung von u(x) + v(x) ist u'(x) + v'(x)

   Ist eine Funktion eine Summe von Teilfunktionen, so ist deren Ableitung die Summe der Ableitungen dieser Teilfunktionen:

   f(x) = x7 + x4 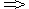f'(x) = 7x6 + 4x3 f(x) = x7 + x4 + x2 + x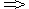 f'(x) = 7x6 + 4x3 + 2x + 1 f(x) = 2x5 - 10x4 + 6x2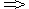 f'(x) = 10x4 - 40x3 + 12x f(x) = 9x3 + x2 - 3x + 90000 f'(x) = 27x2 + 2x -3

Das Ableiten von Polynomen sollte man üben, bis man es im Schlaf kann, denn so gut wie jede Aufgabe erfordert es zuerst, die gegebenen Funktionen abzuleiten. Die Zeit, die man sich hier sparen kann, braucht man dringend in den komplizierteren Teilaufgaben.

Die zweite Ableitung

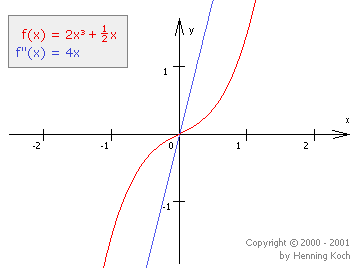
Der zweiten Ableitung f''(x), also der "Steigung der Steigung", kommt ebenfalls eine wichtige geometrische Bedeutung zu: Sie gibt nämlich die Krümmung einer Funktion an:

• Je größer |f''(x₀)|, desto "stärker gekrümmt" ist f(x) um x₀.
• Ist f''(x₀) = 0, so ähnelt f(x) um x₀ einer Geraden.

An dieser Beispielfunktion sieht man das ganz deutlich:

Man unterscheidet zwischen positiver (links-gekrümmter) und negativer (rechts-gekrümmter) Krümmung:

Berechnung höherer Ableitungen

Um die zweite Ableitung einer Funktion zu erhalten, leitet man einfach die erste Ableitung noch einmal mit den obigen Regeln ab. Für die dritte Ableitung leitet man die Zweite noch einmal ab, für die Vierte die Dritte, usw. Beispiel:

f(x) = 8x5 - 4x3 + 9x2 + 44 f'(x) = 40x4 - 12x2 + 18x f''(x) = 160x3 - 24x + 18 f'''(x) = 480x2 - 24 f(4)(x) = 960x f(5)(x) = 960 f(6)(x) = 0 f(7)(x) = 0 f(7)(x) = 0 f(1000000000000)(x) = 0

Wie man sieht ist die Ableitung jeder ganzrationalen Funktion ab f^{(Grad von f + 1)}(x) = 0.

Einige Aufgaben zu diesem Kapitel warten auf ihre Lösung!

Nächstes Kapitel:
2.3.4 Monotonie