3.1 Definitionslücken

Ganzrationale Funktionen besitzen, soweit nicht anders angegeben, die Menge der reellen Zahlen als Definitionsbereich, d.h. wir können jedes x in ein Polynom einsetzen und erhalten den entsprechenden Funktionswert. Eine gebrochenrationale Funktion ist jedoch ein Quotient zweier Funktionen:

f(x) =      g(x)     h(x)

Da durch die Zahl 0 niemals dividiert werden darf, ist f(x) für alle Nullstellen der Nennerfunktion
h(x) nicht definiert, dort befindet sich eine Definitionslücke.

Das Ermitteln der Definitionslücken

Beim Untersuchen gebrochenrationaler Funktionen sollte man immer als allererstes den Definitionsbereich der Funktion ermitteln. Dazu setzt man schlicht und einfach das Polynom h(x) = 0 und errechnet die Lösungen wie in Kapitel 2.3.1 beschrieben (Zerlegungssatz) und hoffentlich zur Genüge geübt.

Beispiel

Wir üben die Ermittlung des Definitionsbereiches an einer einfachen Beispielfunktion:

f(x) =      x + 1     x2 – x – 6

Wir rechnen die Lösungen der Nennerfunktion x² - x - 6 aus:

• x₁ = 3
  
• x₂ = -2

= \ { 3, -2 }

Graphenverlauf um eine Definitionslücke

Wie sieht der Funktionsgraph um eine Definitionslücke herum aus? Es ist bekannt:

• f(x) wird umso größer, je kleiner h(x).
• Je mehr man sich an eine Nullstelle von h(x) annähert, desto kleiner wird h(x).

Daraus folgt, dass f(x) immer größer wird, je näher x an eine Nullstelle x₀ von h(x) herankommt. Theoretisch wäre f(x₀) = , doch ist f(x₀) natürlich nicht definiert. Man nennt deswegen die Definitionslücken einer gebrochenrationalen Funktion auch Unendlichkeitsstellen oder Pole.

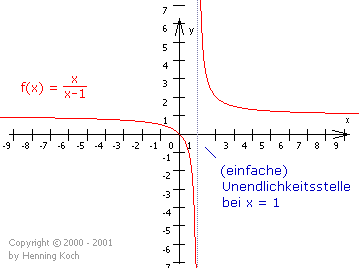
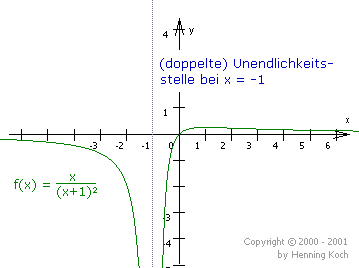
Zur Veranschaulichung die Graphen zweier gebrochenrationaler Funktionen:

Man erkennt hier auch den Unterschied zwischen einfachen, und doppelten Unendlichkeitsstellen: Liegt eine Unendlichkeitsstelle einmal, dreimal, fünfmal, usw., also ungeraden Grades vor, so wechselt der Graph an der Unendlichkeitsstelle sein Vorzeichen.

Liegt eine Unendlichkeitsstelle hingegen zweimal, viermal, sechsmal, usw., also geraden Grades vor, wechselt der Graph an der Unendlichkeitsstelle sein Vorzeichen nicht. Der Graph kommt dann sozusagen aus der Richtung wieder zurück, in der er an der Unendlichkeitsstelle hin "verschwunden" ist.

Pole sind Asymptoten

Hat der Graph bei x = x₀ einen Pol, so sagt man auch, der Graph hat eine senkrechte Asymptote bei x= x₀. Asymptoten sind Geraden, an die sich die Funktion im Unendlichen annähert. Wir werden später, wenn wir das Verhalten im Unendlichen gebrochenrationaler Funktionen behandeln, auch schräge und horizontale Asymptoten kennenlernen.

Einige Aufgaben zu diesem Kapitel warten auf ihre Lösung!

Nächstes Kapitel:
3.2 Nullstellen