Eine Funktion f(x) heißt an einer Stelle x0 ![]()
![]() stetig,
wenn gilt:
stetig,
wenn gilt:
|
Geht man also von zwei Seiten her unendlich nahe an einen Stelle heran, so muss der gleiche Wert wie an dieser Stelle selbst herauskommen. Anschaulich auf die ganze Funktion bezogen bedeutet das, dass f(x) keine Sprungstellen oder Lücken hat. Den Graphen einer stetigen Funktion kann man also in einem Zug, ohne Absetzen des Stiftes zeichnen:
 |
 |
Stetigkeit rationaler Funktionen
Man kann sich hier als Regeln einprägen:
- Die Graphen ganzrationaler Funktionen können nirgends abreißen und sind so immer auf ganz
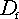 =
= 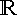 stetig.
stetig.
- Da gebrochenrationale Funktionen an unstetigen Stellen (Definitionslücken, Unendlichkeitsstellen) nicht
definiert sind, sind sie zwar immer auf
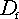 aber
nicht auf ganz
aber
nicht auf ganz  stetig!
stetig!
Die Gruppe der rationalen Funktionen ist also immer auf ihrem Definitionsbereich, jedoch nicht immer auf
![]() stetig. Beim Untersuchen einer rationalen Funktion interessiert uns deshalb nur die Stetigkeit
auf
stetig. Beim Untersuchen einer rationalen Funktion interessiert uns deshalb nur die Stetigkeit
auf ![]() .
.
Stetigkeit abschnittsweise definierter Funktionen
Abschnittsweise definierte Funktionen gehören, wie bereits
erwähnt, nicht zur Gruppe
der rationalen Funktionen, weswegen
die Regel "auf ganz ![]() stetig" hier so nicht anwendbar ist.
stetig" hier so nicht anwendbar ist.
Sind die einzelnen Teilfunktionen einer abschnittsweise definierten Funktion selbst rationale Funktionen, so sind diese auf ihrem jeweiligen Definitionsbereich stetig. Nun müssen aber noch die Übergänge zwischen den einzelnen Teilfunktionen auf Stetigkeit überprüft werden.
Beispiel
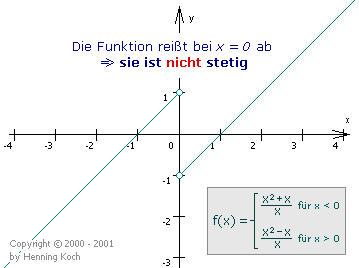
Wir wollen eine abschnittsweise definierte Funktion auf ihre Stetigkeit in ![]() hin untersuchen:
hin untersuchen:
|
Die Funktion f(x) ist also auf ![]() nicht stetig. Sie reißt bei der
Übergangsstelle x = -1 ab, wie ein Blick auf den Graphen sofort bestätigt:
nicht stetig. Sie reißt bei der
Übergangsstelle x = -1 ab, wie ein Blick auf den Graphen sofort bestätigt:
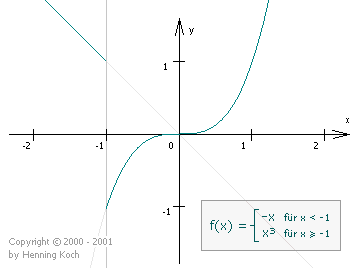 |
Sätze über stetige Funktionen
Eine in einem abgeschlossenen Intervall J = [a;b] stetige Funktion f(x)...
- ... ist innerhalb von J nach oben und unten beschränkt und nimmt somit in J einen
größten und einen kleinsten Funktionswert an, also ein Maximum bzw. Minimum (Extremwertsatz)
- ... nimmt jeden Wert zwischen f(a) und f(b) mindestens einmal an
(Zwischenwertsatz)
- ... hat innerhalb von J mindestens eine Nullstelle, wenn ihre Funktionswerte an den Rändern a und b verschiedene Vorzeichen haben (Nullstellensatz)
Die drei Sätze sollen an einem Beispiel veranschaulicht werden:
 |
Stetig fortsetzbare Funktionen
Beim Kürzen gebrochenrationaler Funktionen haben wir festgestellt, dass Definitionslücken nicht immer Unendlichkeitsstellen sein müssen. Kann man den betreffenden Linearfaktor (x - x0) aus dem Nenner herauskürzen, finden wir an der Definitionslücke einfach ein Loch im Definitionsbereich:
 |
Oft kann man dieses Loch "stopfen" und f(x) zu einer stetigen Funktion ergänzen,
indem man eine Funktion ![]() bildet, die diese Definitionslücke nicht mehr enthält.
Eine Definitionslücke bei x = x0 ist stetig fortsetzbar, wenn gilt:
bildet, die diese Definitionslücke nicht mehr enthält.
Eine Definitionslücke bei x = x0 ist stetig fortsetzbar, wenn gilt:
|
Eine Definitionslücke bei x = x0 ist demnach stetig fortsetzbar, wenn man von beiden Seiten an die Definitionslücke immer näher herangehen kann, und nach dem Grenzwertübergang zweimal den gleichen Wert erhält. An dieser Stelle kann f(x) bei x = x0 stetig ergänzt werden.
Wir nehmen das Beispiel von oben:
|
Wir können jetzt ![]() als abschnittsweise definierte Funktion schreiben:
als abschnittsweise definierte Funktion schreiben:
|
Man denke daran, dass die Möglichkeit einer Bildung von ![]() die Funktion f(x) nicht stetig macht,
sondern nur stetig fortsetzbar.
Einfache "wegkürzbare" Definitionslücken sind immer stetig fortsetzbar, mehrfache Definitionslücken jedoch nicht.
die Funktion f(x) nicht stetig macht,
sondern nur stetig fortsetzbar.
Einfache "wegkürzbare" Definitionslücken sind immer stetig fortsetzbar, mehrfache Definitionslücken jedoch nicht.
|
Nächstes Kapitel:
4.3 Ableitung und Differenzierbarkeit
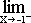 f(–1) =
f(–1) = 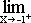 f(–1) = f(–1)?
f(–1) = f(–1)?