Lokale Randextrema
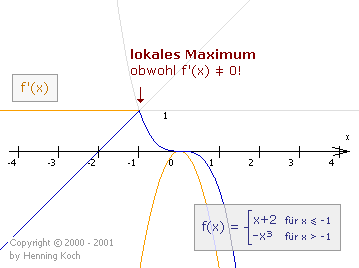
Ist eine abschnittsweise definierte Funktion an den Abschnittsrändern stetig, so kann auf diesen Rändern ein lokales Extremum liegen, auch wenn die uns bekannten Bedingungen für einen lokalen Extremwert nicht vorliegen:
 |
Vorraussetzungen für einen lokalen Extremwert an der Stelle x0 sind in diesem Fall:
- Stetigkeit von f(x) bei x0
- Vorzeichenwechsel von f'(x) bei x0
Um die Art des Randextremums zu bestimmen, untersucht man den Vorzeichenwechsel von f'(x) am Abschnittsrand und vergleicht die Ergebnisse wie in Kapitel 2.3.5 gelernt.
Rechenbeispiel
Wir wollen nun zur Überprüfung die Funktion aus der obigen Illustration auf lokale Extremwerte hin untersuchen:
|
Die Steigung von f(x) ändert sich also bei x = -1 vom Positiven ins Negative, womit die Funktion ein lokales Randmaximum bei x = -1 besitzt!
Globale Randextrema
Wie wir aus Kapitel 3.8 wissen, ist das globale Maximum der höchste Wert, das globale Minimum der kleinste Wert einer Funktion.
Dabei genügte es bisher zur Berechnung der globalen Extremwerte, alle gefundenen lokalen Minima bzw. Maxima miteinander zu vergleichen und jeweils den kleinsten bzw. größten Wert zu wählen. Bei abschnittsweise definierten Funktionen müssen die globalen Extremwerte jedoch nicht mehr unbedingt auf lokalen Extremas liegen:
 |
Wir müssen also die Y-Werte der lokalen Maxima und Minima auch mit den Funktionswerten an den Abschnittsrändern vergleichen. Liegt der niedrigste bzw. höchste Wert der Funktion an einem Abschnittsrand, so spricht man von einem globalen Randextremum. Wie man an dem Bild sieht, muss die Funktion an der Stelle eines globalen Randextremums nicht stetig sein!
Grenzstellen zwischen zwei Teilfunktionen müssen von beiden Seiten her geprüft werden, denn beide anliegenden Teilfunktionen könnten an dieser Stelle ein globales Maximum, bzw. Minimum haben. Dabei muss man genau darauf achten, ob die einzelnen Intervallsgrenzen ein- oder ausschließend sind. Ist ein Abschnittsrand nicht in der entsprechenden Teilfunktion enthalten, muss man sich mittels Grenzwertrechnung an die undefinierte Stelle herantasten.
Ein Rechenbeispiel hierfür finden Sie in der Musteraufgabe im nächsten Kapitel.
|
Nächstes Kapitel:
4.5 Kurvendiskussion und Musteraufgabe
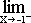 f(x) =
f(x) = 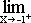 f(x) = f(–1) ?
f(x) = f(–1) ?